基础知识
1.图像如何产生
图像数字化:将模拟图像经过离散化后,得到用数字表示的图像。图像的数字化包括两个过程:采样和量化。
采样:将在空间上连续的图像转换成离散的采样点的操作,即空间坐标的离散化。
量化:把取样后所得的个像素的灰度值从模拟量到离散量的转换操作,即灰度的离散化。
灰度级:表示像素明暗程度的整数量。例如:像素的取值范围为0-255,就称该图像为256个灰度级的图像。
层次:表示图像实际拥有的灰度级的数量。例如:具有32种不同取值的图像,可称该图像具有32个层次。(图像数据的实际层次越多,视觉效果就越好)
对比度:一幅图像中灰度反差的大小。
清晰度:与之有关因素,亮度,对比度,尺寸大小,细微层次,颜色饱和度。
2.像素间的关系
相邻像素
- 4领域($N_4$(p)表示像素p的4领域) 即像素p上下左右四个面
- D领域($N_D$(p)表示像素p的对角领域)即像素p的对角上的像素
- 8领域($N_8$(p)表示像素p的8领域) 即4领域加D领域
邻接性(V是具有特定相似性准则的灰度值集合)
- 4邻接(对于具有值V的像素p和q,如果q在集合$N_4$(p)中,则称这两个像素是4邻接的)
- 8邻接(对于具有值V的像素p和q,如果q在集合$N_8$(p)中,则称这两个像素是8邻接的)
- m邻接(以下条件满足其一即可)
- q在集合$N_4$(p)中
- q在集合$N_D$(p)中,并且$N_4$(p)与$N_4$(q)的交集没有值V的像素
$D_4$距离(城市距离)
像素p(x,y)和q(s,t)之间的$D_4$的距离定义为:
$$D_4(p,q)=|x-s|+|y-t|$$
$D_8$距离(棋盘距离)
像素p(x,y)和q(s,t)之间的$D_8$的距离定义为:
$$D_8(p,q)=max(|x-s|,|y-t|)$$
基本运算
1.点运算
点运算:运算结果只跟像素点自己有关,有它的灰度值确定。
邻域运算:运算结果不仅与像素点自己有关,还与该像素的多个邻接像素的灰度值有关。
变换域运算:主要指频率域的处理方法,主要指低通和高通滤波器。迪通滤波用来消除噪声,高通滤波用来提升边缘、轮廓。
在图像增强中,传统的方法一般很少用到邻域运算。
在图像平滑中,肯定要用到领域运算,只有通过邻域才能判断该像素是否含有噪声,并用适当的方法消除噪声。
在边缘检测中,肯定要用到邻域运算,通过邻域来判定该像素是否是边缘
点运算包括:线性灰度变换,分段线性灰度变换,非线性灰度变换(对数变换,指数变换)
灰度级分层(两种基本方法):1.将感兴趣范围内的所有灰度值显示为一个值,而将其他灰度值显示为另一个值。2.使感兴趣范围的灰度变量(或变暗),而保持图像中的其他灰度级不变。
图像亮度:图像矩阵灰度的平均值,其值越小图像整体越暗。
$$brightness=\frac{\sum_{y=0}^{M-1}\sum_{x=0}^{N-1}f(x,y)}{M\times N}$$图像对比度:图像矩阵的均方差(标准差)。对比度越大,图像中黑白反差越明显。
$$contrast=\sqrt{\frac{\sum_{y=0}^{M-1}\sum_{x=0}^{N-1}(f(x,y)-brightness)^2}{M \times N}}$$
直方图
直方图:对图像灰度分布统计的重要手段。
直方图修正:通过修改直方图的形状达到图像增强目的。
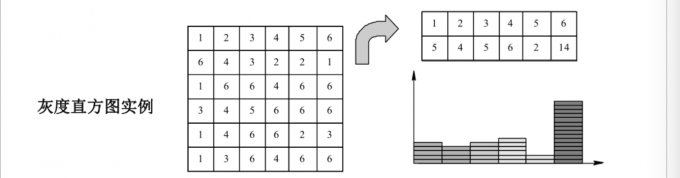
- 灰度直方图:表示图像中具有某种灰度级的像素个数,反映图像中每种灰度出现的频率。一般的,灰度直方图的横坐标是灰度级,纵坐标是该灰度级出现的次数,是图像最基本统计特征。
直方图的性质:
- 未反映某一灰度值像素所在位置,即丢失了位置信息。
- 图像与直方图之间是多对一的映射关系。
- 一幅图像各子区的直方图之和等于该图像全图的直方图。
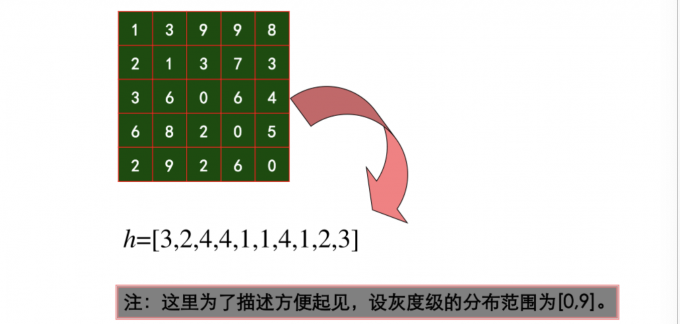
直方图的计算
- 初始化:hist[k]=0;k=0…L-1
- 统计:hist[f(x,y)]++;x=0,…,M-1;y=0,…,N-1
- 归一化:hist[f(x,y)]/=M*N
直方图均衡化
均衡化的目的是使每个h[i]都相等(图像信息量最大),就是把原始图像的直方图变换为均匀分布的形式。
考虑两种情况(图像像素个数n,有效灰度级个数L)
- 多个至一个:若有连续n个灰度级的频数之和等于n/L,则必导致它们合并成一个灰度级。
- 一个到多个:若有某个灰度级的频数是n/L的R倍,则必须将其分为R个不同的灰度级,每个上都有n/L个像素。
求解步骤:
分析
- 均衡化后的结果不是均衡的,因为只合并并不分解。
- 信息量没有增加,反而减少量。因为均衡化后图像的有效灰度级一般<L
- 优点:能自动增强整个图像的对比度
- 缺点:具体增强效果不易控制
直方图规定化:把直方图变换为某个特定形状,有选择地增强某个灰度范围内的对比度。假设原图像为f,直方图规定化后得到的图像为g,待匹配(参考)图像为m,则直方图规定化的步骤为
- 求f和m的归一化灰度直方图,记为$h_f$和$h_m$
- 对f和m计算累积直方图
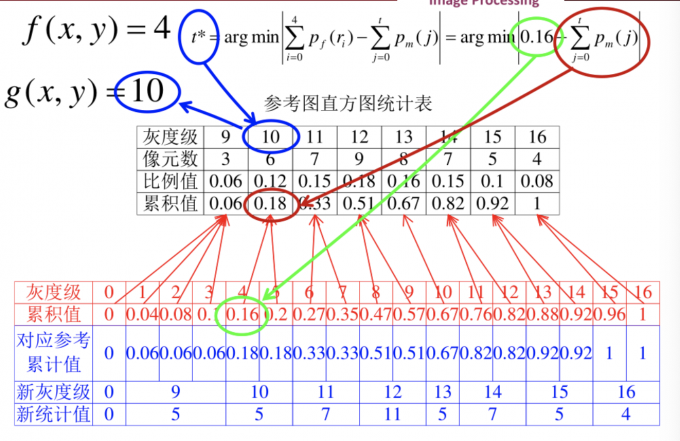
- 对每个像素值f(x,y),找到使式(2)最小对$t^*$,即为规定化后得到的灰度值g(x,y),即式(1)
$$g(x,y)=t^* \quad \quad \quad(1)$$
$$t^*=arg min|T_f(f(x,y))-T_m(t)|
=arg min|\sum_{i=0}^{f(x,y)}p_f(r_i)-\sum_{j=0}^{t}p_m(j)| \quad \quad \quad(2)$$
解释:原图像的累积值减去参考图像的累积值的最小值(如,原灰度级为4,对应累积值为0.16,-参考图0.06为0.1,减去0.18为-0.02,减去0.33为-0.17,因此最小值为-0.02,对应新灰度级为10)
直方图均衡化vs直方图规定化
直方图均衡化:
- 自动增强
- 效果不易控制
- 总得到全图增强的结果
直方图规定化: - 有选择地增强
- 须给定需要的直方图
- 可特定增强的结果
直方图均衡化可以看作目标直方图为均匀分布的直方图规定化。
2.算数运算
- 加法
给整幅图像增加灰度级会使图像亮度得到提高,整体变亮,给个别像素增加灰度值可以使目标景物突出。(通过M幅图像相加再取平均,可以去除叠加性噪声) - 减法
- 图像分割:分割运动的车辆,减法去掉静止部分,剩余的是运动元素和噪声。
- 去除不需要的叠加性元素。
- 显示两幅图像的差异,检测同一场景两幅图像之间的变化。
- 乘法
可以改变图像的灰度级范围(如原来是10-100的灰度级范围,乘以2则是20-200的灰度级范围),图像与图像相乘,定义为图像卷积运算(应用:图像的局部显示,用二值模板图像与愿图像做乘法)
3.逻辑运算
- 非逻辑
$$g(x,y)=255-f(x,y)$$
应用:
1.获得一个阴图像
2.获得一个子图像的补图像。
- 与逻辑
$$k(x,y)=f(x,y) \wedge g(x,y)$$
应用:
1.求两个子图像的相交子图
2.获得一个子图像的补图像。
- 或逻辑
$$k(x,y)=f(x,y) \vee g(x,y)$$
应用:
1.合并子图像
- 异或逻辑
$$k(x,y)=f(x,y) \oplus g(x,y)$$
应用:
1.获得相交子图像
4.几何运算
几何变换基于矩阵运算
图像的位置变换是指图像的平移、镜像与旋转。
应用:主要是用于目标识别中的目标配准。
图像的形状变换是指图像的放大、缩小与错切。
按比例放大:如果需要将愿图像放大k倍,则将一个像素值填在新图像的$k \times k$的子块中。
任意不成比例放大:这种操作由于x方向和y方向的放大倍数不同,一定带来图像的几何畸变。
图像放大倍数太大,会出现马赛克效应。(解决:图像矢量化,超分辨率)
错切:实际上是平面景物在投影平面上的非垂直投影效果。错切之后原图像的像素排列方向改变。与前面旋转不同的是,x方向与y方向独立变化。
-
图像的仿射变换是指图像集合变换的描述。
其次坐标表示:
所谓其次坐标就是将一个原本是n维的向量用一个n+1维向量来表示。
通常都采用归一化的齐次坐标,即取h=1.(x,y)的规格化其次坐标为(x,y,1)。
其次坐标的几何意义:可理解为在三维空间上第三维为常数的一平面上的二维向量。
其次坐标作用:
- 将各种变换用阶数统一的矩阵来表示:提供了用矩阵运算把二维、三维甚至高维空间上的一个点从一个坐标系变换到另一个坐标系的有效方法。
- 便于表示无穷远点。例如:$(xh,yh,h)$,令h=0,即便是n维空间的一个无穷远点。
几何变换-插值
分为:前向映射和逆向映射。
最近邻插值
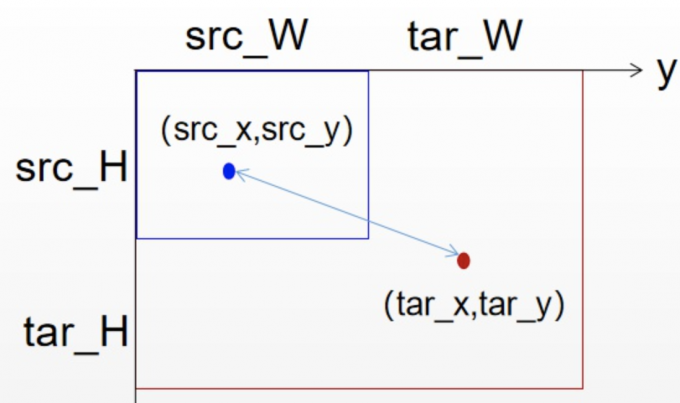
其中src表示原始图像,tar表示插值得到的目标图像,H和W分别表示图像的高度和宽度。插值的核心是找到(tar_x, tar_y)和(src_x, src_y)的映射关系,从而实现对目标图像的每一个像素点进行赋值。假设目的是将原始图像长度和宽度扩大(3,4)倍,即:
1 | ratio_H = tar_H/src_H = tar_x/src_x = 3 |
通过上式变形,得到目标图像的像素点和原始图像的像素点映射如下:
1 | tar_x = src_x*ratio_H |
如h表示变换后图像,f表示原图像
$$h(tarX,tarY)=f(\frac{tarX}{3},\frac{tarY}{4})$$
进行4舍5入到原图像的点。
缺点:
- 放大后的图像有很严重的马赛克,会出现明显的块状效应
- 缩小后的图像有很严重的失真。
双线性插值
线性插值:使用谅解两个已知量的直线来确定在这两个已知量之间的一个未知量的值。线性插值形式: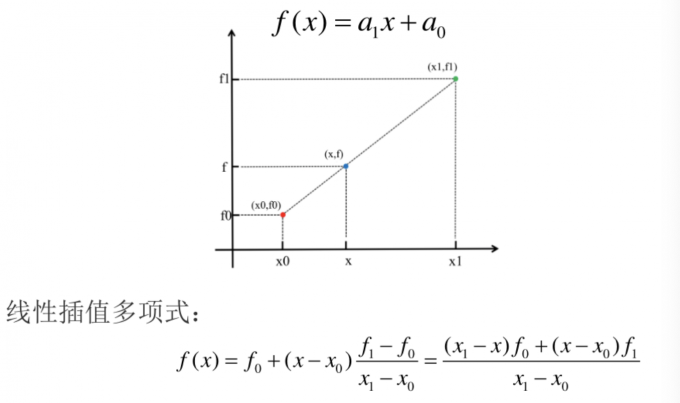
双线性插值是线性插值在二维时的推广,在两个方向上工做了三次线性插值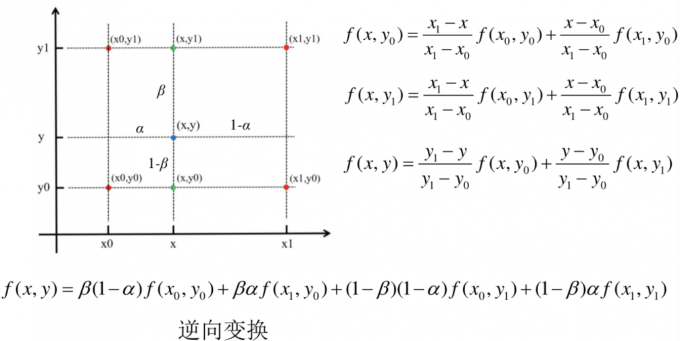
简记:某点乘以它不相连的两条边。
输出图像上每个点的像素值是多个分配值叠加而成的,不能保证所有分配到其上的权重之和为1.因此必须记录下所有分配到其上的权重并累加起来,最后利用累加权重进行归一化,才能得到正确的插值结果。
特殊问题
图像卷绕(扭曲):图像卷绕是通过指定一系列控制点的位移来定义空间变换的图像变形处理。非控制点的位移根据控制点插值确定。
图像变形:变形是使图像中的一个物体逐渐变形为另一物体的过程。