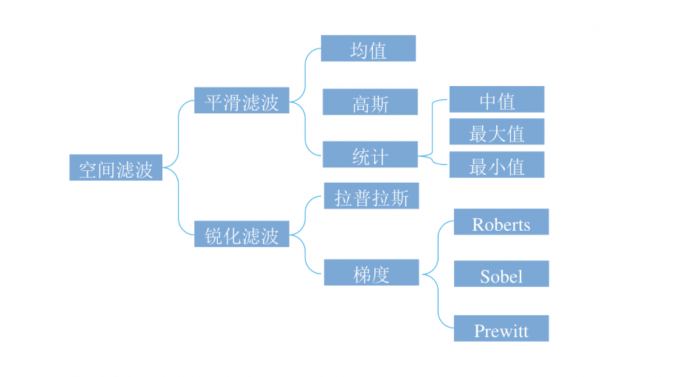
空间域图像增强
内容大致：
4.空间滤波
空间滤波：使用空间模板进行的图像处理。
空间滤波器：模板本身。
分类
- 平滑滤波器、低通滤波器，作用：边缘平滑、去噪。
- 锐化滤波器、高通滤波器，作用：边缘提取与增强。
低通滤波去除了图像的高频部分，即细节信息，留下的低频信息代表了概貌。常用例子，比如美图秀秀的磨皮，去掉了脸部细节信息（痘坑，痘印，暗斑等）。
1.平滑滤波器
平滑空间滤波器的分类
- 线性滤波器：均值滤波器、高斯滤波。
- 非线性滤波器：中值滤波器、最大值滤波器、最小值滤波器。
平滑空间滤波器的作用：
- 模糊处理：去除图像中一些不重要的细节。
- 减少噪声
图像噪声：定义和描述方式
噪声是妨碍人们感觉器官对所接收信源信息理解的因素。噪声在理论上可定义为“不可预测，只能用概率统计方法来认识的随机误差”。噪声可用随机过程及其概率分布函数和概率密度函数，通常用其数字特征，即均值方差、相关函数等进行处理。
图像噪声的特点
- 噪声在图像中的分布和大小不规则，即随机性。
- 噪声与图像之间具有相关性。
- 噪声具有叠加性。
图像噪声分类
- 按其产生的原因：外部噪声和内部噪声。
- 按统计特性：平稳噪声和非平稳噪声。
- 按噪声和信号之间的关系：加性噪声和乘性噪声。
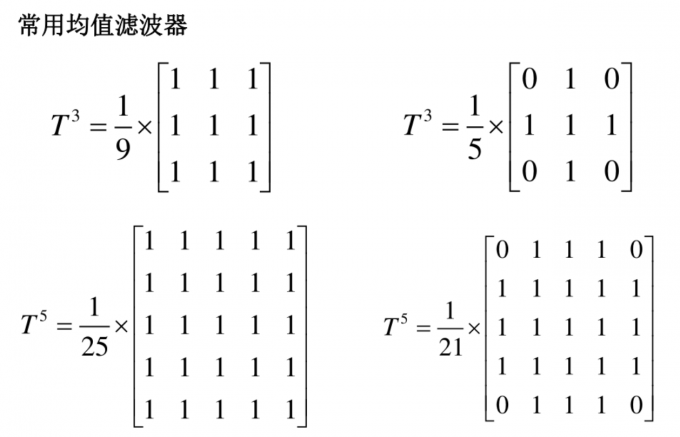
均值滤波
对于一个滑动窗口内的各像素灰度级求平均值、用该均值来代替窗口中心像素的灰度值。比如：
$$g(x,y)=\frac{f(x-1,y)+f(x,y)+f(x+1,y)}{3}$$
均值滤波的关键是设计合理的滤波器，包括形状和大小。
作用：
- 减小图像灰度的“尖锐”变化，减小噪声。
- 由于图像边缘是由图像灰度尖锐变化引起的，所以也存在边缘模糊的问题（局限性）。
常用滤波器：
运用滤波器，滤波器窗口（3x3，5x5）越大，平滑的越厉害，模糊也越严重。
均值滤波的一个重要应用是为了对感兴趣的物体得到一个粗略的描述，模糊一幅图像。
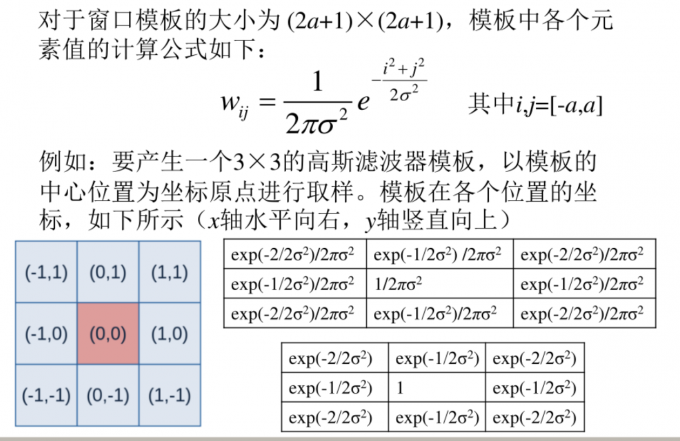
高斯滤波
一种特殊的线性滤波，其使用高斯函数作为权函数。
$$p(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{-x^2}{2\sigma^2}}$$
$\sigma$值的意义及选取
高斯滤波器模板的生成最重要的参数就是高斯分布的标准差$\sigma$。标准差代表着数据的离散程度，如果$\sigma$较小，那么生成的模板的中心系数较大,而周围的系数较小，这样对图像的平滑效果就部署很明显；反之，$\sigma$较大,则生成的模板的各个系数相差就不是很大，比较类似均值模板，对图像的平滑效果比较明显。
均值滤波和高斯滤波特点
- 系数之和等于1。
- 系数都是非负。
- 执行速度快。
- 容易造成图像模糊。实质上在求平均过程中，噪声的灰度值也加入了均值当中，从而向周围扩散，导致图像模糊，边缘不清晰。
- 滤波前后图像亮度不变。
统计排序滤波器
定义：是一种非线性滤波器，基于滤波器所在图像区域中像素的排序，由排序结果决定的值代替中心像素的值。
分类：
- 中值滤波器：用像素邻域内的中间值代替该像素。
- 最大值滤波器：用像素邻域内的最大值代替该像素。
- 最小值滤波器：用像素邻域内的最小值代替该像素。
中值滤波
定义：对于一个滑动窗口内nm个像素按灰度值进行排序，用中值来替代窗口中心像素原来的灰度。
$$g(x,y)=median f(s,t)$$
作用：强迫突出的亮点（暗点）更像它周围的值，以消除孤立的亮点（暗点）。
思考：为什么中值滤波更好地保持了边缘？其边缘没有模糊？
解释：在目标和背景边界处的像素，当其邻域中大多数为目标点时，他就取目标的灰度值，当其邻域中大多数为背景点时，它就取背景的灰度值，因此不模糊。
中值滤波特点
- 计算复杂度高（排序），执行速度慢。
- 滤波前后图像亮度发生改变（但非常接近）
- 不容易造成图像模糊，具有非常好的抗噪性能。中值滤波能够在抑制随机噪声的同时不使边缘模糊。
极值滤波
最大值滤波
对于一个滑动窗口mn内的各像素求灰度值最大值，用该最大值来替代窗口中心像素原来的灰度值。
$$g(x,y)=max f(s,t)$$
最小值滤波
对于一个滑动窗口mn内的各像素求灰度值最小值，用该最小值来替代窗口中心像素原来的灰度值。
$$g(x,y)=min f(s,t)$$
2.锐化滤波器
定义：使模糊图像变清晰，增强图像的边缘等细节。一般先去除噪声，再进行锐化处理。
微分滤波器的原理：
均值产生钝化的效果，而均值与积分相似，由此而联想到，微分能不能产生相反的效果，即锐化的效果？
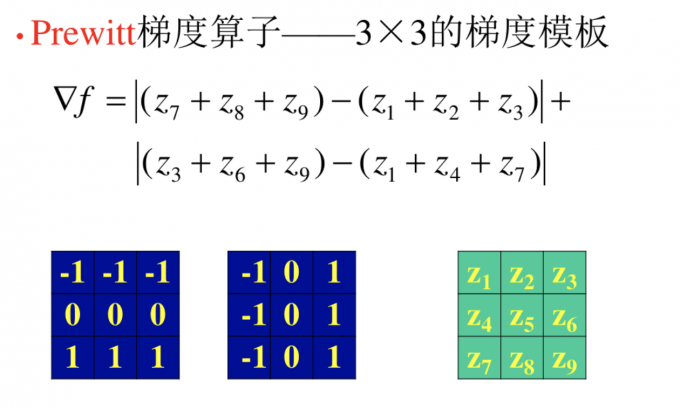
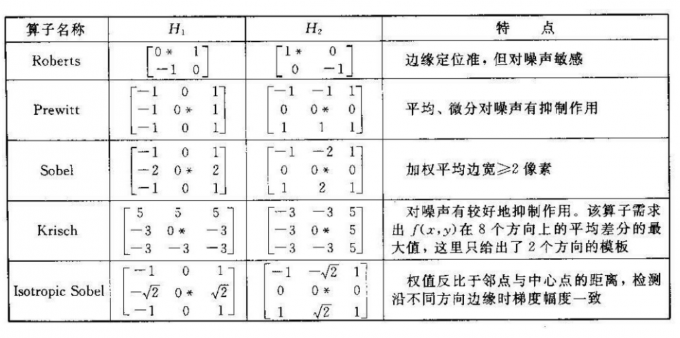
1.Roberts交叉梯度算子
2.Sobel梯度算子
这里有个错误，上图中应改为（$z_1+2z_2+z_3$）
Sobel梯度算子的计算方法具体参考这篇文章
3.Prewitt梯度算子
4.常用梯度算子
5.拉普拉斯算子
注意点：
