1.集合的平移
由集合A中所有元素平移后组成的元素集合称为集合A的平移，记为$(A)_z$
$$(A)_z={w|w=a+z,a\in A}$$
其中，w表示集合A中的元素a平移z后形成的元素。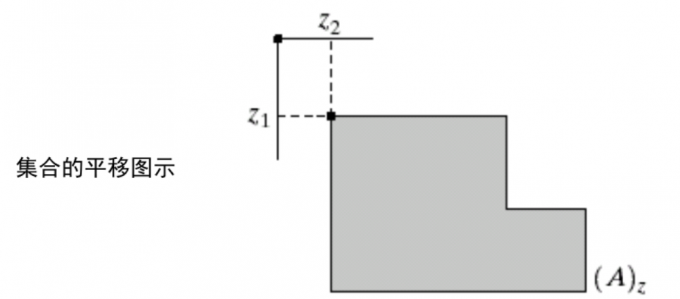
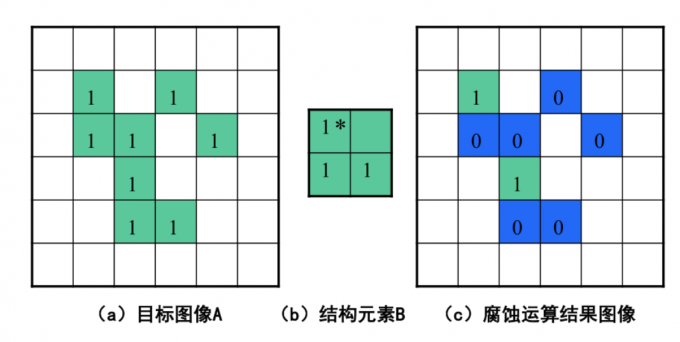
2.膨胀与腐蚀–腐蚀
腐蚀：A被B腐蚀的定义为:
$$A \ominus B= {z|(B)_z \subseteq A}$$
该式表明腐蚀的结果为所有使B中包含于A中的点z的集合用z平移。集合B在被称为结构元素。
等价形式：
$$A \ominus B={z|(B)_z \cap A^c = \varnothing}$$
腐蚀运算的含义是：每当在目标图像A中找到一个结构元素B相同的子图像时，就把该子图像中与B的原点位置对应的那个像素位置标注为1，图像A上标注出的所有这样的像素组成的集合，即为腐蚀运算的结果。
简而言之，腐蚀运算的实质就是在目标图像中标出那些与结构元素相同的子图像的原点位置的像素。
注意，结构元素中的原点位置可以不为1。
将目标图像进行缩小
结构元素形状对腐蚀运算结果的影响
腐蚀运算的结果不仅与结构元素的形状（矩形、圆形、菱形等）选取有关，而且还与原点位置的选取有关。
腐蚀运算的应用
利用腐蚀算法消除物体之间的粘连示例
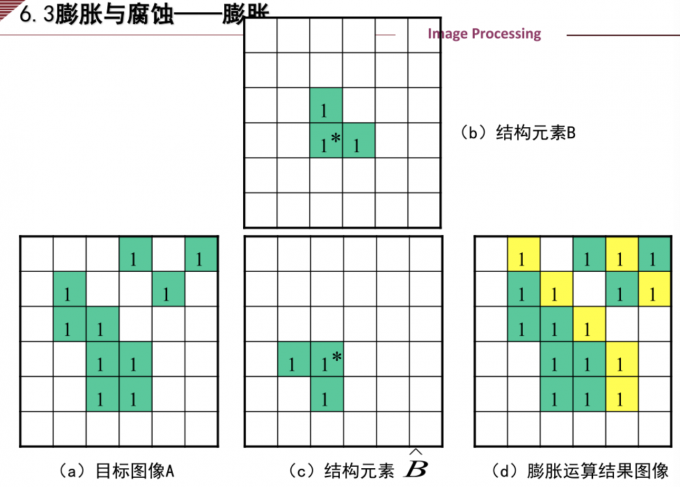
3.膨胀与腐蚀–膨胀
膨胀：A被B膨胀的定义为：
$$A \oplus B = {z | (B)_z \cap A \neq \varnothing }$$
该式表明膨胀过程是B首先做关于原点的映像，然后平移z。A被B膨胀是所有位移z的集合，这样B和A至少有一个元素是重叠的。
腐蚀是一种收缩或细化操作，而膨胀则会“增长”或“粗化”
将目标图像进行扩展1
结构元素形状对腐蚀运算结果的影响
当目标图像不变，但所给的结构元素的形状改变时；或结构元素的形状不变，而其原点位置改变时，膨胀运算的结果会发生改变。
膨胀运算的应用
利用膨胀运算将相邻的物体连接起来
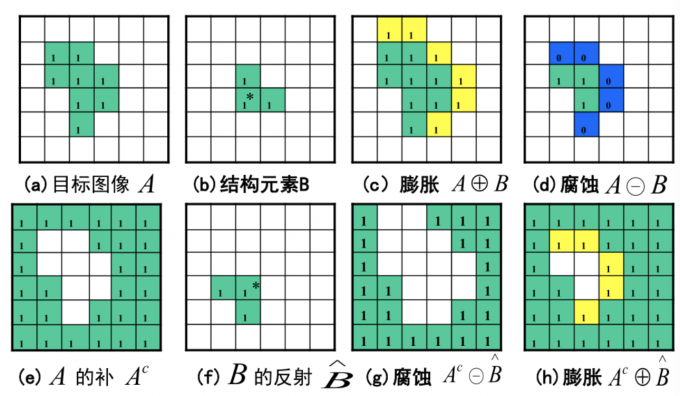
腐蚀运算与膨胀运算的对偶性-示例
原目标图像A进行膨胀(腐蚀)与目标图像的补的腐蚀(膨胀)相同。
4.开闭运算–开操作
定义：使用同一个结构元素对目标图像先进行腐蚀运算，然后再进行膨胀运算称为开操作。
开操作一般使对象的轮廓变得光滑，断开狭窄的间断和消除细的突出物。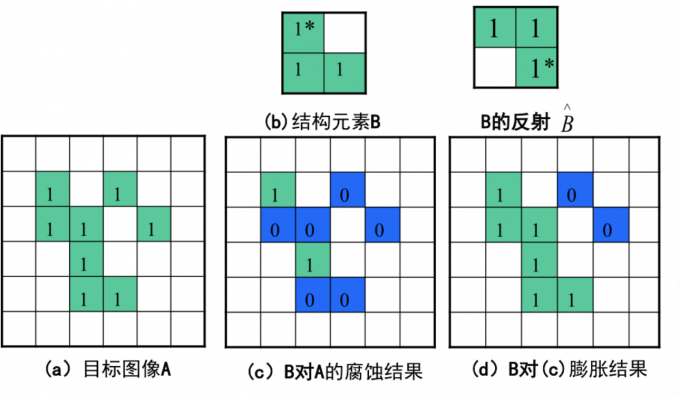
5.闭操作
定义：使用同一个结构元素对目标图像先进行膨胀运算，然后再进行腐蚀运算称为闭操作。
闭操作同样使轮廓线更光滑，但它通常消弭狭窄的间断和长细的鸿沟，消除小的孔洞，并填补轮廓线中的断裂。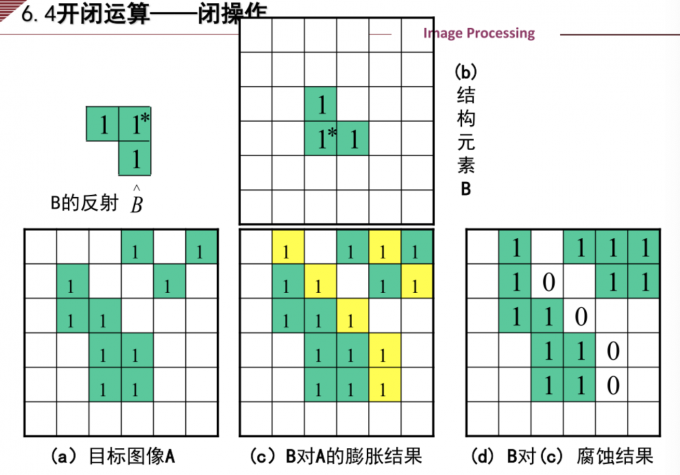
上图腐蚀有点问题
6.击中或击不中变换
击中或击不中变换是形状检测的基本工具。
在某些应用中，我们可能对检测某个集合内由1和0组成的某些模式感兴趣，在这种情况下不需要背景。因此，击中或击不中就简化为简单的腐蚀。
可以参考这篇文章
7.形态学应用
- 边界提取
- 孔洞填充
- 连通分量的提取
- 凸壳
- 细化
- 粗化
- 骨架
- 裁剪
8.灰度级形态学
- 腐蚀膨胀
- 开闭操作
- 顶帽变换、底帽变换
