频率域图像增强
为什么要在频率域研究图像增强?
- 可以利用频率成分和图像外表之间的对应关系。一些在空间域表述困难的增强任务,在频率域中变得非常普通。
- 滤波在频率域更为直观,它可以解释空间域滤波的某些性质
- 可以在频率域指定滤波器,做逆变换,然后在空间域使用结果滤波器作为空间域滤波器的指导,一旦通过频率试验选择了空间滤波,通常实施都在空间域进行。
傅立叶变换
性质:
- 平移性质
- 分配律
- 尺度变换
- 旋转性
- 周期性和共轭对称性
- 平均值
- 可分性
- 卷积
频率域图像增强
- 低通滤波器
- 高通滤波器
傅立叶变换的频率分量和图像空间特征之间的联系
- 变化最慢的频率成分(u=v=0)对应一幅图像的平均灰度级
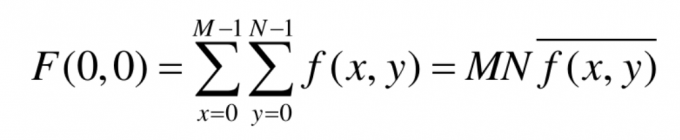
- 当从变换的原点移开时,低频对应着图像的慢变化分量,如图像的平滑部分。
- 进一步离开原点时,较高的频率对应图像中变化越来越快的灰度级,如边缘或噪声等尖锐部分。
频率域的滤波步骤
- 用$(-1)^{x+y}乘以输入图像进行中心变换f(x,y)(-1)^{x+y} \leftrightarrow F(u-M/2,v-N/2)$
- 计算1中的DFT$ F(u,v)$
- 用滤波器函数$H(u,v)$乘以$F(u,v)$
- 计算3中结果的IDFT
- 得到4中结果的实部
- 用$(-1)^{x+y}乘以5中的结果$

